通过虚拟仿真动画的呈现，可以很好地细致地呈现真实信号分解中难以观察到的各个分量的细节，如各次谐波分量的具体变化情况。吉布斯效应随着各次谐波的变化情况，各次谐波的功率、相位变化情况等。
 
1.  实验内容与任务
 
实验内容：
连续时间周期信号（例：方波信号）的傅里叶分解与合成，并对信号进行频谱分析。
实验任务：
掌握傅立叶级数（FS），学会连续时间周期信号的傅里叶分解合成基本原理与频谱分析的方法，掌握其MATLAB实现；
软件上：傅里叶级数展开（信号分解）及基波、一次谐波、二次谐波等的时域信号图及多次谐波的逐次叠加，观察合成信号与原始信号的逼近程度，并观察其中的吉布斯现象。
硬件上：在信号与系统实验箱观察矩形脉冲信号通过多个数字滤波器后，分解出各谐波分量的情况。观察矩形脉冲信号分解出的各谐波分量可以通过叠加合成出原矩形脉冲信号。
 
2.  相关知识及背景
 
周期函数的傅立叶级数的形式，掌握连续时间周期信号的分解与合成原理；
利用符号运算求傅立叶级数的系数,尤其是求积分、变量替换的操作；
通过傅立叶级数求各次谐波分量；
周期信号的频谱分析；
示波器的基本操作。
 
3.  教学目的
 
掌握傅立叶级数（FS），学会分析连续时间周期信号的频谱分析及MATLAB实现；分析典型的矩形脉冲信号，了解谐波分量的构成与合成出原矩形脉冲信号的现象。
 
4.  实验原理及方案
 
    实验基本原理
1.傅里叶级数展开：


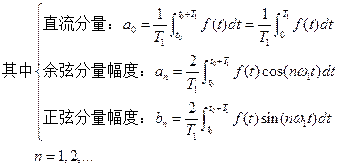
如此完成分解并生成各次谐波。
 
2.各次谐波叠加原理：

 

 
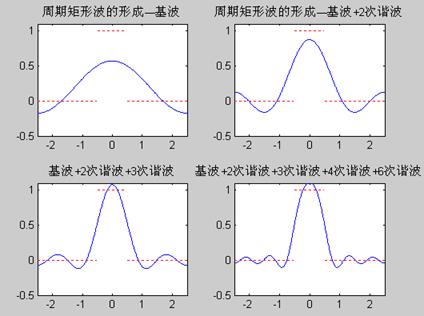
3.周期信号的频谱分析：




 
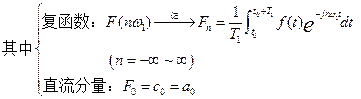
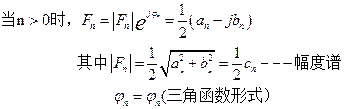
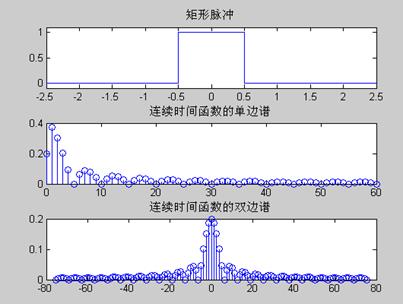
4 选频网络（带通滤波器）实现信号分解
通过一个选频网络可以把电信号中所包含的某一频率成分提取出来。
硬件实验采用同时分析法，基本工作原理是利用多个滤波器，把它们的中心频率分别调到被测信号的各个频率分量上。当被测信号同时加到所有滤波器上，中心频率与信号所包含的某次谐波分量频率一致的滤波器便有输出。在被测信号发生的实际时间内可以同时测得信号所包含的各频率分量。


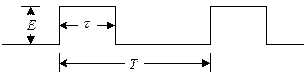一个幅度为E，脉冲宽度为τ，重复周期为T的矩形脉冲信号，如下图所示。

   
其傅里叶级数为：

该信号第次谐波的振幅为：
                   
 
进行信号分解和提取是滤波系统的一项基本任务。当我们仅对信号的某些分量感兴趣时，可以利用选频滤波器，提取其中有用的部分，而将其它部分滤去。
目前DSP数字信号处理系统构成的数字滤波器已基本取代了传统的模拟滤波器，数字滤波器与模拟滤波器相比具有许多优点。用DSP构成的数字滤波器具有灵活性高、精度高和稳定性高，体积小、性能高，便于实现等优点。因此在这里我们选用了数字滤波器来实现信号的分解。
在数字滤波器模块上，选用了有8路输出的D/A转换器TLV5608（U502），因此设计了8个滤波器（一个低通、六个带通、一个高通）将复杂信号分解提取某几次谐波。
分解输出的8路信号可以用示波器观察，测量点分别是TP801、TP802、TP803、TP804、 TP805、TP806、TP807 、TP808。
5. 加法器实现信号合成：
矩形脉冲信号通过8路滤波器输出的各次谐波分量可通过一个加法器，合成还原为原输入的矩形脉冲信号，合成后的波形可以用示波器在观测点TP809进行观测。如果滤波器设计正确，则分解前的原始信号（观测TP501）和合成后的信号应该相同。
 
完成实验任务的思路方法
 
软件实验采用MATLAB 2011b，需要掌握的技巧包括符号运算（尤其是积分函数int，变量替换subs等函数的使用方式）；数值运算；图形绘制函数与图形叠加绘制的方法。
 
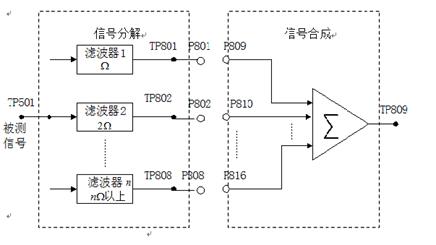
给出一个连续时间周期信号——方波信号，如下图：

 
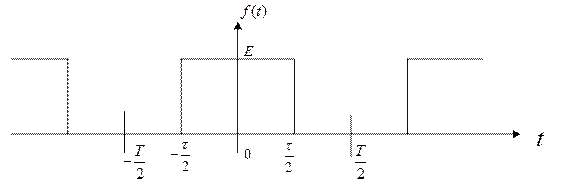
其中，=5，=1，E=1
 
1. 软件实验方案步骤为：
1. 利用heaviside函数描述一个周期的方波信号；
2. 利用积分函数，完成傅里叶级数的直流、正弦、余弦的各次谐波系数的符号表达式；
3. 利用变量替换，获得各次谐波系数，利用各次谐波的表达式计算各次谐波的数值向量；
4. 利用plot函数绘制各次谐波完成波形分解；
5. 将各次谐波进行逐次叠加，hold on与plot，观察谐波叠加后与原始方波的区别，从而讨论吉布斯效应
6. 利用各次谐波分量系数，构建以各次谐波为横轴的单边频谱、双边频谱的幅度谱图。
 
2. 硬件实验方案步骤为：
2.1、信号分解:
1．将J701置于“脉冲”位置，连接P702与P101；
2．按下选择键SW101，此时在数码管SMG101上将显示数字，继续按下按钮，直到显示数字“5”。
3．矩形脉冲信号的脉冲幅度和频率按要求给出，改变信号的脉宽，测量不同时信号频谱中各分量的大小。
示波器可分别在TP801、TP802、TP803、TP804、TP805、TP806、TP807和TP808上观测信号各次谐波的波形。
 
2.2信号合成:
1．输入的矩形脉冲信号，（的矩形脉冲信号又称为方波信号），。
2．电路中用8根导线分别控制各路滤波器输出的谐波是否参加信号合成，用导线把P801与P809连接起来，则基波参于信号的合成。用导线把P802与P810连接起来，则二次谐波参于信号的合成，以此类推，若8根导线依次连接P801－P809、P802－P810、 P803－P811、P804－P812、P805－P813、P806－P814、P807－P815、P808－P816，则各次谐波全部参于信号合成。另外可以选择多种组合进行波形合成，例如可选择基波和三次谐波的合成；可选择基波、三次谐波和五次谐波的合成等等。
3．在输出端观察和记录合成结果，调节电位器W805可改变合成后信号的幅度。
 
5.  实验报告要求
实验目的、实验内容、实验仪器、实验原理（连续时间周期信号的傅里叶级数展开、各次谐波的理论计算、叠加方法）、电路实验过程的基本设计和观察数据的表格设计。实验结果的数据分析应能观察到各次谐波，谐波叠加后对方波的逼近程度，吉布斯效应的观察与说明。
 
6.  项目特色或创新
信号与系统难学难懂的问题，是因为概念丰富、理论复杂、公式繁多，且理论与实际没有很好的结合，很多实验设计停留在数学到数学层面。本实验将傅里叶级数展开理论直观地在实际信号的分解与合成中呈现出来，且通过软硬件结合的方式，让学生进一步加深理论联系实际，理论指导实践，巩固和加深同学们对课程内容的理解。